鬼滅の刃の幾何学模様シェル芸とは?
こういう画像を出すシェル芸です。
炭治郎
禰豆子
善逸 。
。
やっていきましょう。
前提条件はimagemagickがインストールされていることです。
炭治郎
作りたい画像
コマンドができるまで
ステップ0. 作りたい画像を観察する
画像をよく見て、性質を捉え、作る方法を考えます。
実際はこの段階では完成した画像は無いわけなので、炭治郎をよく見てください。
そうすると
赤く囲んだ部分を単位として、大きなキャンバスにしきつめることでこの画像になりそうですね。
ステップ1. タイルを作る
黒と緑が互い違いになったタイルを作りましょう。
コマンド
$ convert <(echo P3 2 2 1 0 0 0 0 1 0 0 1 0 0 0 0)-scale 10000% /images/0.png
出力画像
200x200のタイルができました。echo P3 2 2 1 0 0 0 0 1 0 0 1 0 0 0 0は、無圧縮PPMフォーマットで、
横2ピクセルx縦2ピクセルの、黒と緑の画像を出力します。
最初のP3 2 2 1はPNMのヘッダです。P3が無圧縮のRGB(PPM)画像であることを示します。
続く2 2 1は画像のサイズが2x2であり、画素値が最大1(0または1の2値)であることを示します。
残りの0 0 0 0 1 0 0 1 0 0 0 0はデータ部分で、3つの数値が1ピクセルのRGB値になっています。
3つごとに区切ると0 0 0→黒, 0 1 0→緑,0 1 0→緑,0 0 0→黒で、
それぞれ左上、右上、左下、右下のピクセルの色になります。convert <(echo P3 2 2 1 0 0 0 0 1 0 0 1 0 0 0 0)で、2x2画像をconvertに入力します。
コマンドの続きは-scale 10000%となっています。これはは100倍拡大です。
ステップ2. タイルを繰り返す
できたタイルを単位として、大きなキャンバスに繰り返し貼り付けて敷き詰めます。
コマンド
$ convert <(echo P3 2 2 1 0 0 0 0 1 0 0 1 0 0 0 0)-scale 10000% -write mpr:a +delete -size 1000x1000 tile:mpr:a /images/x.png
出力画像
完成ですね。
前ステップのコマンドの続きは -write mpr:a +deleteとなっています。
これでタイルをmpr:aに格納して、いったんイメージシーケンスを空にしています。
その続きは-size 1000x1000 tile:mpr:aとなっています。
これで1000x1000のサイズに、mpr:aのタイルを敷き詰めたものができます。
完成したコマンド
$ convert <(echo P3 2 2 1 0 0 0 0 1 0 0 1 0 0 0 0)-scale 10000% -write mpr:a +delete -size 1000x1000 tile:mpr:a /images/x.png
別解1
$ convert <(echo P3 2 2 1 0 0 0 0 1 0 0 1 0 0 0 0)-scale 10000% -define distort:viewport=1000x1000 -virtual-pixel tile -distort srt 0 /images/x.png
-virtual-pixel tileを使う方法。
mprに格納して、いったんイメージシーケンスをクリアする、
っていうのをやらないで済む。
別解2
$ convert <(echo P3 2 2 1 0 0 0 0 1 0 0 1 0 0 0 0)-scale 10000% miff:-|convert -size 1000x1000 tile:- /images/x.png
miff(magick image file format)で出力してパイプすることで、
mpr格納とイメージシーケンスクリアをしなくて済むし、
別解1より実行も早い(理由はよくわからない)。
シェル芸らしさ(?)も高い感じがする。
禰豆子
作りたい画像
コマンドができるまで
ステップ0. 作りたい画像を観察する
今回もタイルの繰り返しで画像を作れるでしょうか?
赤で囲った部分をタイルとして繰り返すことで作れそうですね。
さらに赤い部分は
黄色で囲った部分を上下左右に反転して結合すると作れそうですね。
ステップ1. 黄色囲み部分を作る
黄色で囲った部分を作りましょう。
コマンド
$ convert -size 86x50 xc:pink -stroke black -fill none -draw'polyline 0,0 0,49 28,0 85,0 0,49 57,49 85,0 85,49' /images/0.png
出力画像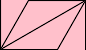
-size 86x50 xc:pinkで86x50のピンク色のキャンバスを作っています。
86x50は、だいたいcos30°:sin30°になるようにしています。-stroke blackで、図形を描く時の輪郭線を黒にしています。-fill noneで、図形を描くときの塗りつぶしを無しにしています。-draw 'polyline …'で、polyline以降の座標で表された点を結ぶ折れ線(多角形)を描きます。
ステップ2. 赤囲み部分を作る
赤で囲んだ部分を作りましょう。
コマンド
$ convert -size 86x50 xc:pink -stroke black -fill none -draw'polyline 0,0 0,49 28,0 85,0 0,49 57,49 85,0 85,49'\( +clone -flop\) +append \( +clone -flip\)-append /images/1.png
出力画像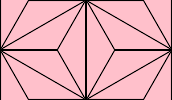
\( +clone -flop \) +appendは、前ステップの黄色囲み部分のコピーを左右反転して、横に結合しています。\( +clone -flip \) -appendは、さらにそのコピーを上下反転して、縦に結合しています。
ステップ3. タイルを繰り返す
あとは炭治郎と同じです。
$ convert -size 86x50 xc:pink -stroke black -fill none -draw'polyline 0,0 0,49 28,0 85,0 0,49 57,49 85,0 85,49'\( +clone -flop\) +append \( +clone -flip\)-append-write mpr:a +delete -size 800x800 tile:mpr:a /images/x.png
完成したコマンド
$ convert -size 86x50 xc:pink -stroke black -fill none -draw'polyline 0,0 0,49 28,0 85,0 0,49 57,49 85,0 85,49'\( +clone -flop\) +append \( +clone -flip\)-append-write mpr:a +delete -size 800x800 tile:mpr:a /images/x.png
別解1
$ convert -size 86x50 xc:pink -stroke black -fill none -draw'polyline 0,0 0,49 28,0 85,0 0,49 57,49 85,0 85,49'-define distort:viewport=800x800 -virtual-pixel mirror -distort srt 0 /images/x.png
-virtual-pixel mirrorを使う方法。
黄色囲み部分からいきなり完成形にいける。
別解2
$ convert -size 86x50 xc:pink -stroke black -fill none -draw'polyline 0,0 0,49 28,0 85,0 0,49 57,49 85,0 85,49'\( +clone -flop\) +append \( +clone -flip\)-append miff:-|convert -size 800x800 tile:- /images/x.pn
miffを使う方法。やはり別解1より実行が早い。
線の太さが気になる人へ
「なんか線の太さが一定じゃないのが気になる」という人向けのコマンド
線太さ2の場合のコマンド
$ convert -size 86x50 xc:pink -stroke black -strokewidth 2 -fill none -draw'polyline -0.5,-0.5 -0.5,49.5 28,-0.5 85.5,-0.5 -0.5,49.5 57,49.5 85.5,-0.5 85.5,49.5'\( +clone -flop\) +append \( +clone -flip\)-append miff:-|convert -size 800x800 tile:- /images/y.png
$ convert -size 86x50 xc:pink -stroke black -strokewidth 1 -fill none -draw'polyline -0.5,-0.5 -0.5,49.5 28,-0.5 85.5,-0.5 -0.5,49.5 57,49.5 85.5,-0.5 85.5,49.5'\( +clone -flop\) +append \( +clone -flip\)-append miff:-|convert -size 800x800 tile:- /images/z.png
出力画像
今回詳しく説明はしませんが
「ピクセルは点ではない」
「画像の左上隅の頂点は、ピクセル座標の(0,0)ではなく(-0.5,-0.5)である」
っていう話が関係しています。
善逸
作りたい画像
コマンドができるまで
ステップ0. 作りたい画像を観察する
白三角が規則的に並んでる画像と、黄色から赤のグラデーション画像をうまいこと結合するとこれができそうですね。
白三角が規則的に並んでる画像は、
青で囲んだ部分を繰り返せばできそうですね。
さらに青で囲んだ部分は、
赤で囲んだ部分を、幅の半分だけ横にずらして(はみ出した部分は反対側から出てくるイメージ)、縦に結合すればできそうですね。
ステップ1. グラデーションを作る
コマンド
$ convert -size 1000x1000 gradient:yellow-orangered /images/0.png
出力画像
gradient:yellow-orangeredで、黄色からオレンジレッドのグラデーションを作っています。
ステップ2. 赤囲み部分を作る
コマンド
$ convert -size 66x58 xc:black -fill white -draw'polyline 33,0 13,34 53,34' /images/0.png
出力画像
-draw 'polyline …'で多角形(三角形)を描いています。
ステップ3. 青囲み部分を作る
コマンド
$ convert -size 66x58 xc:black -fill white -draw'polyline 33,0 13,34 53,34'\( +clone -roll +33+0 \)-append /images/2.png
出力画像
前ステップのコマンドに続けて\( +clone -roll +33+0 \)することで、
赤囲み部分の幅の半分(33ピクセル)だけ横にずらしたものを作って、-appendで縦に結合しています。
ステップ4. タイルを繰り返す
$ convert -size 66x58 xc:black -fill white -draw'polyline 33,0 13,34 53,34'\( +clone -roll +33+0 \)-append-write mpr:a +delete -size 1000x1000 tile:mpr:a /images/3.pn
出力画像
前ステップのコマンドに続けて-write mpr:a +deleteすることでmpr:aに格納して、イメージシーケンスをクリア、-size 1000x1000 tile:mpr:aすることで、1000x1000のサイズで、mpr:aをタイルとして繰り返しています。
ステップ5. 結合する
ステップ1のグラデーションとステップ4の白三角繰り返し画像をうまいこと結合します。
コマンド
$ convert -size 66x58 xc:black -fill white -draw'polyline 33,0 13,34 53,34'\( +clone -roll +33+0 \)-append-write mpr:a +delete -size 1000x1000 tile:mpr:a \(-size 1000x1000 gradient:yellow-orangered \)-compose lighten -composite /images/x.png
出力画像
完成ですね。-compose lightenで結合の方法を指定して、-compositeで結合しています。
lightenは二つの画像のピクセル値の明るい方を使う結合方法ですね(たぶん)。
なので、黒と他の色なら、他の色の方が使われ、白と他の色なら白の方が使われます。
完成したコマンド
$ convert -size 66x58 xc:black -fill white -draw'polyline 33,0 13,34 53,34'\( +clone -roll +33+0 \)-append-write mpr:a +delete -size 1000x1000 tile:mpr:a \(-size 1000x1000 gradient:yellow-orangered \)-compose lighten -composite /images/x.png
別解1
$ convert -size 66x58 xc:black -fill white -draw'polyline 33,0 13,34 53,34'\( +clone -roll +33+0 \)-append-define distort:viewport=1000x1000 -virtual-pixel tile -distort srt 0 \(-size 1000x1000 gradient:yellow-orangered \)-compose lighten -composite /images/x.png
-virtual-pixel tileを使って繰り返す方法。
別解2
$ convert -size 66x58 xc:black -fill white -draw'polyline 33,0 13,34 53,34'\( +clone -roll +33+0 \)-append miff:-|convert -size 1000x1000 tile:- <(convert -size 1000x1000 gradient:yellow-orangered miff:-)-compose lighten -composite /images/x.png
miffを使う方法。白三角繰り返し画像をパイプで渡して、グラデーション画像を<でリダイレクトしています。<(convert -size 1000x1000 gradient:yellow-orangered miff:-)の:-)の部分がかわいいですね。
冨岡さん
今回詳しく説明しませんけど、冨岡さんも一応やりました。
コマンド
$ convert -size 344x150 xc:yellow -stroke blac出力画像k -fill none -draw'polyline 0,0 0,100 86,150 86,50 0,0'-draw'polyline 0,25 0,100 63,137 63,62 0,25'-draw'polyline 172,0 86,50 86,150 172,100 172,0'-draw'polyline 172,25 107,62 107,137 172,100 172,25'-fill orange -draw'polyline 0,50 0,100 43,125 43,75 0,50'-draw'polyline 172,50 129,75 129,125 172,100 172,50'-fill mediumseagreen -draw'polyline 172,0 172,100 258,150 258,50 172,0'-draw'polyline 344,0 258,50 258,150 344,100 344,0'-fill darkgreen -draw'polyline 0,0 86,50 172,0'-draw'polyline 86,150 172,100 258,150'\( +clone -roll +86+0 \)-append\( +clone -roll +172+0 \)-append miff:-|convert -size 1000x1000 tile:- /images/x.png
出力画像
もっと工夫して短く書けそうな感じはしますが、今回はここまで。
まとめ
鬼滅の刃に出てくる幾何学模様は、imagemagickで簡単に描ける!(やつもあるし難しいのやつもある)
所感
書いているうちにmiffの使い方を知ったので、当初考えていたよりもちょっとテクニカルな感じになりましたね。




